Diese Seite funktioniert nur mit Javascript.
Inputs und Outputs, fixe und variable Faktoren3.2.2 Das klassische ErtragsgesetzDurchschnitts- und Grenzprodukt
as klassische Ertragsgesetz ist eine Produktionsfunktion ( klassisches Ertragsgesetz) Es kann herangezogen werden, um Produktionsprozesse zu beschreiben, bei denen ein Produktionsfaktor variiert wird, während alle anderen konstant gehalten werden. Dann spricht man von partieller Faktorvariation. Es eignet sich aber auch zur Beschreibung der Produktion, bei der alle Faktoren variiert werden (wobei natürlich eine "gleichmäßige" Variation der einzelnen Faktoren erfolgt, so dass das Einsatzverhältnis der Faktoren untereinander konstant bleibt). In diesem Fall spricht man von totaler Faktorvariation ( Ertragskurve bei totaler Faktorvariation).
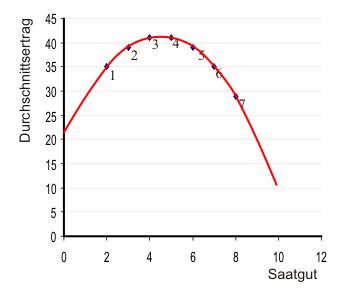
Zur Erläuterung des klassischen Ertragsgesetzes dient folgendes (hypothetisches) Beispiel: Abbildung 1 zeigt Ergebnisse eines kontrollierten Experiments einer landwirtschaftlichen Forschungsanstalt. Simuliert wurde auf 7 Feldern die partielle Faktorvariation eines Saatgutes, d.h. Feldgröße, Düngereinsatz etc. wurde konstant gehalten. Dabei wurden auf dem ersten Feld 2 Einheiten Saatgut ausgebracht; die Ausbringungsmenge auf den weiteren sechs Feldern wurde schrittweise bis auf 8 Einheiten ausgedehnt. Wiedergegeben ist der gemessene durchschnittliche Ertrag pro Einheit Saatgut. Es lässt sich ablesen, dass der Durchschnittsertrag mit je 41 Einheiten auf den Feldern 3 und 4 am größten war.
Das Beispiel zeigt, dass es so etwas wie eine "optimale" Saatmenge für die Felder gibt - jedenfalls dann, wenn man optimal im Sinne von maximaler Ertrag je ausgebrachter Einheit begreifen möchte.
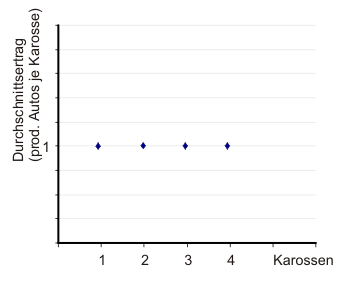
Für viele andere (vor allem industrielle) Produktionsprozesse wäre ein solches Ergebnis kaum denkbar. Abbildung 2 zeigt ein entsprechendes Diagramm für die Automobilproduktion.
In Abbildung 1 liegen die Beobachtungen auf einer Funktion die sich durch die Gleichung
$$ \text{DE} = \cfrac{x}{s} = -s^2 + 9s +21 \tag{1}$$beschreiben lässt. Dabei steht DE für Durchschnittsertrag, $x$ für die Ertragsmenge und $s$ für die Saatgutmenge (Die Funktion wird in Abbildung 1 gezeigt, wenn Sie das Diagramm anklicken). Den Gesamtertrag erhält man offensichtlich, wenn man den Durchschnittsertrag mit dem Faktoreinsatz multipliziert.
$$ x = -s^3 + 9s^2 +21s \tag{2}$$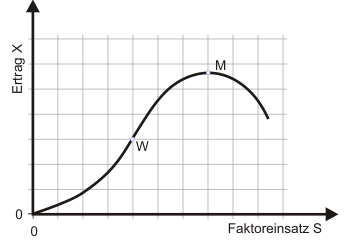
Dies ist die Ertragskurve für Gut X bei partieller Faktorvariation des Saatgutes S. Sie hat die Gestalt des Klassischen Ertragsgesetzes, das in Abbildung 3 schematisch dargestellt ist.
Für Abbildung 3 ist eine schematische Darstellung gewählt, um die Besonderheiten des klassischen Ertragsgesetzes hervortreten zu lassen. In einer maßstabsgetreuen Wiedergabe von Gleichung (2) würde man den Wendepunkt W bei $s = 3$ und das Maximum M bei $s = 7$ finden, allerdings hinterließe die Darstellung nicht so sehr den Eindruck, dass die Kurve dem Verlauf eines zur Seite geneigten S folgt. Auch wenn es vielleicht selbstverständlich sein mag, sei erwähnt, dass die Kurve im Koordinatenursprung beginnt - ein positiver Ordinatenabschnitt würde anzeigen, dass Produktion bei nicht vorhandenem Faktoreinsatz stattfindet. Das kann bei partieller Faktorvariation möglich sein, bei totaler Faktorvariation ist es ausgeschlossen.